二叉树的重建
前面几篇笔记讲了二叉树的表达与遍历。那么,有没可能根据二叉树遍历的结果,来重建出一棵二叉树呢?答案是肯定的。
给出二叉树前序遍历的结果和中序遍历的结果,我们就能根据这些信息,重新生成二叉树。这个问题相对来说有挑战性,需要花费更长的时间来思考。
看下面这棵树:
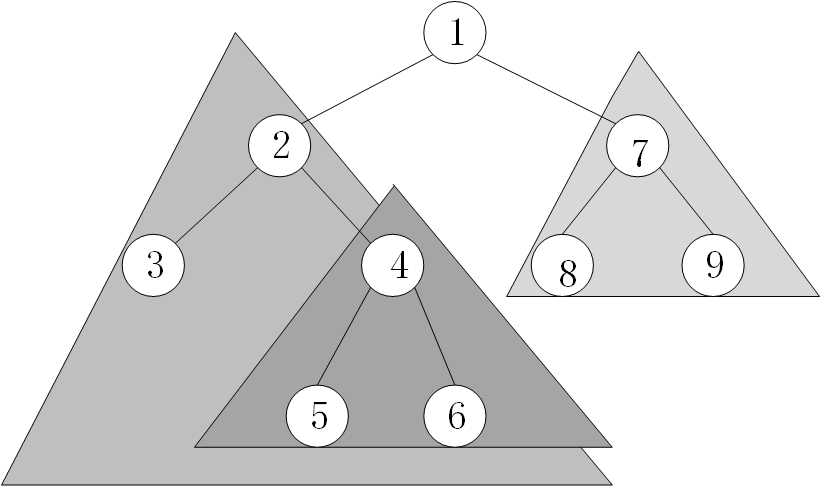
前序遍历结果为pre={1,2,3,4,5,6,7,8,9}
中序遍历结果为in={3,2,5,4,6,1,8,7,9}
我们可以发现,设前序遍历的当前节点为c,则在中序遍历的结果中,c点左侧和右侧就可以构成左子树和右子树。也就是说,把中序结果分成两半了。比如,前序当前为1时,那么中序的3,2,5,4,6都属于以1为父节点的左子树,7,8,9都属于以1为父结点的右子树。以此类推,我们就可以通过递归来重建整棵二叉树。
注意事项
我们在处理递归问题的时候,需要处理好区间边界的问题。也就是说,要明确我们的区间是开区间还是闭区间。不然很有可能就因为这区间的问题而导致程序出错。
而且,临界问题也容易出错。在这个问题里面就是结点的左子结点为空和右子结点为空的情况。所以,我在下面的程序里,用了两个标记变量去标记他们的左右子结点是否为空,为空则把它们指向NIL。
代码实现
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstdio>
using namespace std;
#define MAX 100
#define NIL -1
struct Node
{
int id;
int left;
int right;
bool is_left_null;
bool is_right_null;
};
Node T[MAX];
int n;
vector<int> st,mi;
int pos=0;
Node reconstruct(int left,int right)
{
int root = st[pos];
if(left >= right)
{
Node tmp;
tmp.left = NIL;
tmp.right = NIL;
tmp.id = root;
//处理好边界问题,也就是子节点为空的时候
tmp.is_left_null = true;
tmp.is_right_null = true;
return tmp;
}
pos++;
int m = distance(mi.begin(), find(mi.begin(), mi.end(), root));
Node tmp1 = reconstruct(left,m);
Node tmp2 = reconstruct(m+1,right);
if(tmp1.is_left_null)
{
T[root].left = NIL;
}
else{
T[root].left = tmp1.id;
}
if(tmp2.is_right_null)
{
T[root].right = NIL;
}
else{
T[root].right = tmp2.id;
}
T[root].id = root;
return T[root];
}
/*
void check()
{
for(int i=1;i<=n;i++)
{
if(T[i].left==T[i].right)
{
T[i].left = NIL;
T[i].right = NIL;
}
if(T[i].left==0)
T[i].left = NIL;
if(T[i].right == 0)
T[i].right = NIL;
}
}
*/
void postOrder(int u)
{
if(u==NIL)
{
return;
}
postOrder(T[u].left);
postOrder(T[u].right);
printf("%d", u);
if(u!=st[0])
cout<<" ";
}
int main()
{
for(int i=0;i<MAX;i++)
{
T[i].left = NIL;
T[i].id = NIL;
T[i].right = NIL;
}
cin>>n;
for(int i=0;i<n;i++)
{
int tt;
cin>>tt;
st.push_back(tt);
}
for(int i=0;i<n;i++)
{
int tt;
cin>>tt;
mi.push_back(tt);
}
reconstruct(0,n);
//check();
for(int i=1;i<=n;i++)
{
cout<<"id: "<<T[i].id<<" left: "<<T[i].left<<" right: "<<T[i].right<<endl;
}
cout<<endl;
postOrder(st[0]);
cout<<endl;
}
欢迎关注我的公众号“灯珑”,让我们一起了解更多的事物~

