算法与数据结构之图

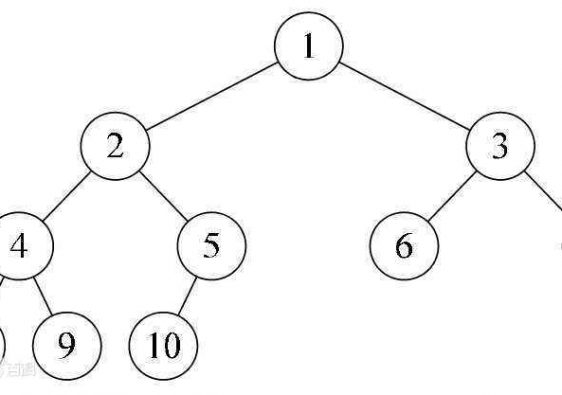
图这种数据结构表现的是对象集合以及其间的关系的集合。

图中的“对象”称为结点(Node)或者顶点(Vertex)，通常用圆来表示。“关系”表示顶点与顶点之间的关系，称为边(Edge)。圆与圆之间的关系用连线或者箭头来表示。

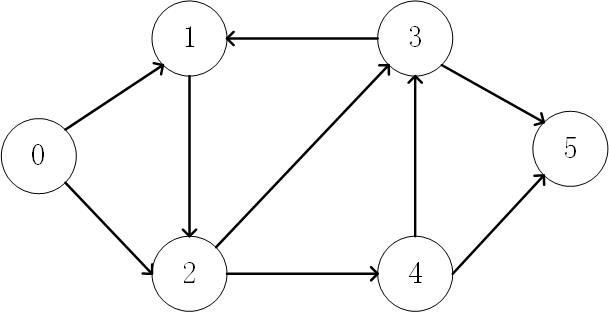
无向图

无向图是边没有方向的图。可以用来表现朋友关系这一类的关系。

有向图

有向图是边有方向的图，比如可以用来表示一件事物的学习顺序，要先学会某样知识才能学下一样知识。

加权无向图

加权的“权”就是给边赋的值。有了权值，我们可以表示诸如两个地点之间的距离这样子的信息。

加权有向图

有了加权有向图，那么就可以为A->B和B->A来设置不同的权值。

图的表述

设顶点的集合为V，边的集合为E的图记作G=(V,E)。并且这个图的定点数和边数分别为|V|、|E|。

连接两个顶点u、v的边记作e = (u, v) ，在无向图之中，(u,v) 和 (v,u)代表同一条边。在加权图中，边 (u, v) 的权值记作 w(u, v)

两个点的相邻：如果无向图中存在边(u, v) ，那就称这两个点相邻。

路径： 一组相邻顶点的序列称为路径。起点和终点相同的路径称为环

不存在环的有向图称为DAG

度：与顶点u相连的边数称为顶点u的度。对于有向图来说还有入度和出度。

连通图：对于有向图而言，如果任意两点u, v之间，都存在使得u能到达v的路径。

子图：对于两个图G和G’，如果G’的顶点集合和边的集合是G的子集，那么称G’是G的子图。

邻接表表示法

邻接表表示法中，对于每个顶点，都用一个邻接表来表示，每个邻接表中的元素表示与当前结点相连的顶点。

邻接矩阵表示法

邻接矩阵表示法用|V|*|V|的矩阵表示图。如果顶点i到顶点j存在边，那么a(ij) = 1，否则为0；

邻接矩阵表示法的优点

·可以通过M[u][v]直接引用边(u, v), 因此只需常数时间O(1)即可确定顶点u和顶点v的关系

·只要更改M[u][v] 就能完成边的添加与删除，简单高效。

邻接矩阵表示法的缺点

·消耗的内存空间等于顶点数的平方。如果图的边数较少（稀疏图），则会浪费大量的内存空间。

·在一个邻接矩阵中，只能记录顶点u到顶点v的一个关系（一个基本型的二维数组中，无法在同一对顶点之间画出两条边）

例题：

ALDS1_11_A

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_11_A

#include<iostream>
using namespace std;

int g[101][101];

int main()
{
    int n;
    cin>>n;

    for(int i=1;i<=n;i++)
    {
        int u;
        cin>>u;
        int k;
        cin>>k;
        for(int j=1;j<=k;j++)
        {
            int v;
            cin>>v;
            g[u][v] = 1;
        }
    }

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cout<<g[i][j];
            if(j!=n) cout<<" ";
            else cout<<endl;
        }
    }



}

欢迎关注我的公众号“灯珑”，让我们一起了解更多的事物~